前一阵子朋友换工作，去了新公司的一个基础服务的部门。对数据结构和算法的要求着实不低，不是平常的CRUD，而是通过各种巧妙的数据结构去完成对应的业务需求。我发现是时候夯实一下基础了，这次来看一下树结构中的线段树。

一、什么是线段树

有一种很经典的线段树问题：区间染色。
讲的是有一面长度为 n 的墙，每次选择一段儿墙进行染色。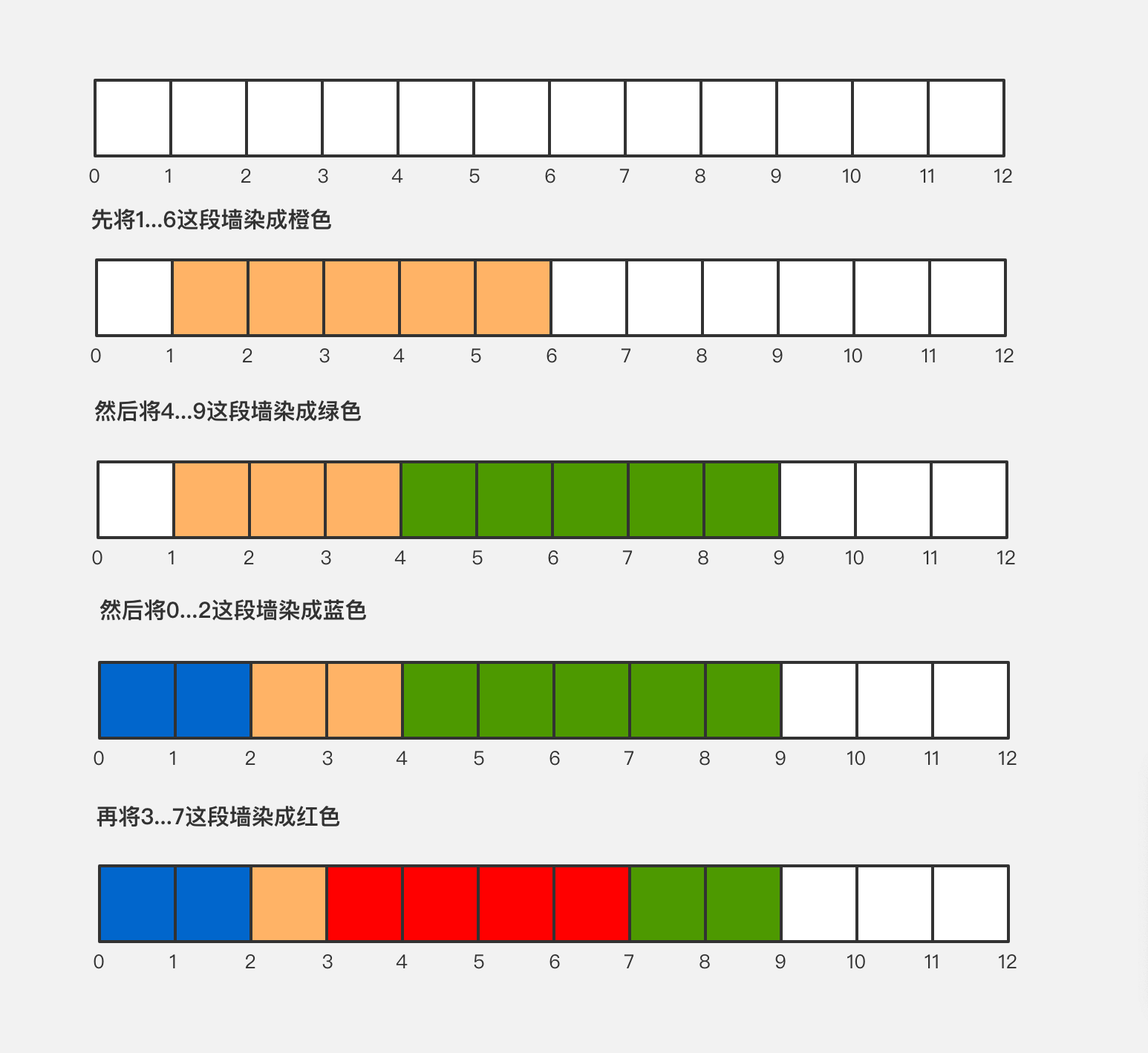

在染色的过程中，会有一部分被重复染色，那么 m 次操作后，我们可以看见多少种颜色呢？在 [i,j] 区间内可以看见多少种颜色呢？
我们可以知道上述的问题是对区间进行以下的操作：

更新区间（染色操作）
查询区间（查询操作）
通过上面的图片描述，我们很容易可以想到利用数组来实现，对于染色操作和查询操作时间复杂度均是是 O(n)。
其实更普遍一点，这一类问题的实质，是基于区间的统计查询。比如一个电商网站，需要看2019年的注册用户消费额最高的用户。这里需要注意，我们关注的是动态的情况，是看在2019年注册的用户在到现在为止消费额的统计量，并不是说在单单在2019年消费最高的。如果是单单2019年消费最高的统计，直接拿出2019年的数据进行统计即可，因为2019年的数据已经是定值了。我们考虑的是动态的情况，是伴随更新的同时进行查询，即既有更新又有查询的操作，此时，使用线段树是一种好的选择。当然依然可以使用普通数组进行实现，只不过使用线段树的时间复杂度会低一些。

	使用数组实现	使用线段树
更新	O(n)	O(logn)
查询	O(n)	O(logn)

我们总结以上讨论的问题场景：

对于给定的区间，支持以下两种操作。

更新：更新区间中一个元素或者一个区间的值
查询一个区间 [i,j] 的最大值、最小值，或者区间数字和等。

那么我们怎么抽象出线段树的数据结构呢？
通过上面的说明，我们是不会像线段树中进行添加和删除元素的，即区间的长度是固定不变的，只是区间中的元素可能会发生变化。所以我们可以使用一个静态数组来表示，线段树具体就是下面的样子。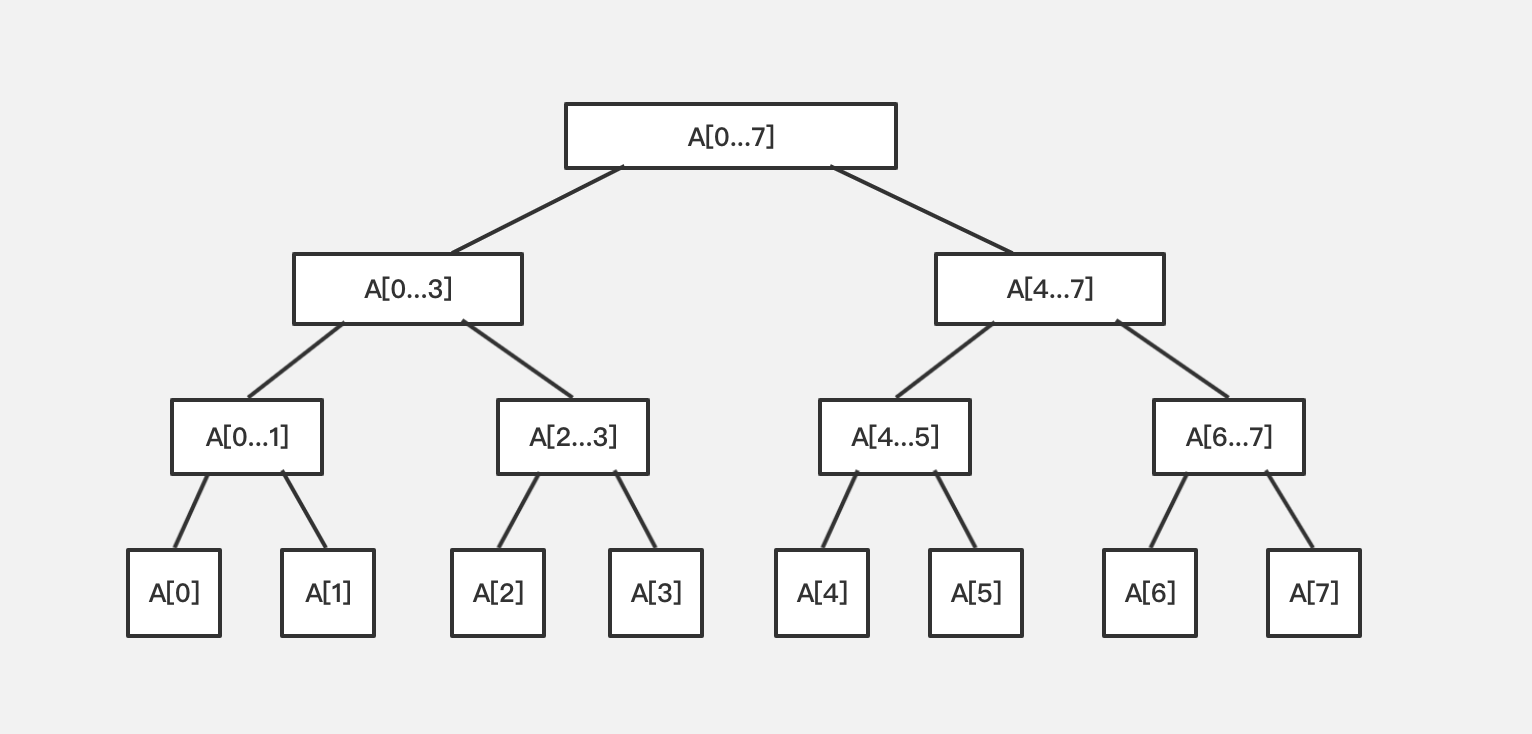

和普通二叉树的区别是，每一个节点所表示的是一个区间内的信息。以求合为例，每一个节点存储的是每个区间相应的数字和，根节点是整个区间的数字和，之后往下分成两个子区间，以此类推，直到最后叶子节点是单个的数字。

当我们需要求[4…7]区间的和，可以很方便的从树中找到，并不需要对数组进行挨个遍历。

二、线段树的表示

在上面线段树有8个叶子节点，比较特殊，正好是一个满的二叉树，如果有10个元素，线段树是下面的情况：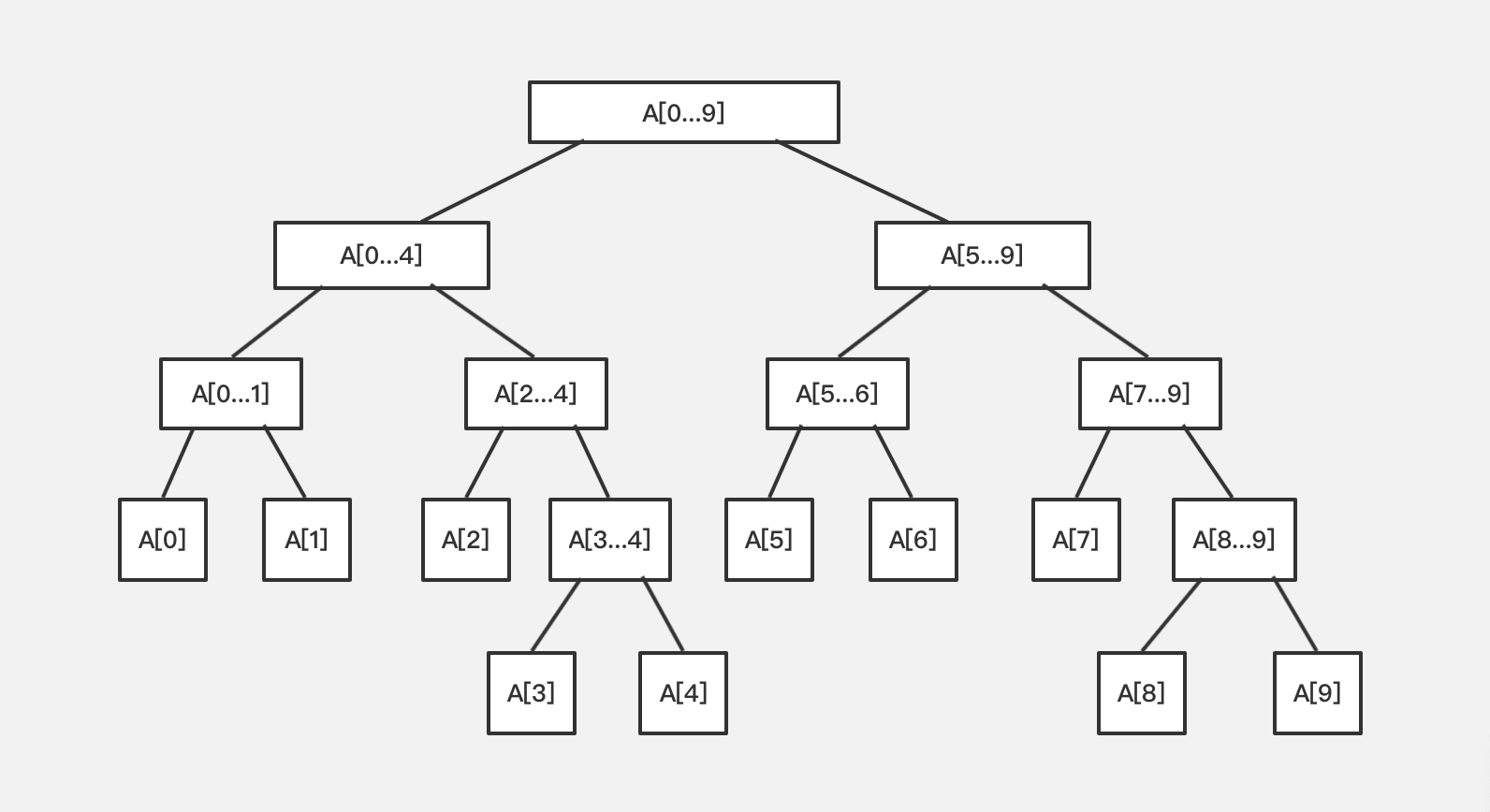

当一个节点不能平均分的时候，这里把这个节点分成一个节点少一点，一个节点多一点。
所以，线段树不是完全二叉树，但是是平衡二叉树。
为了简便，其实我们可以把线段树看作是一棵满的二叉树，只不过最后一层的叶子点有些是空的。满的二叉树我们可以很方便的用数组来表示，那么问题来了，我们需要多少节点来表示这课树呢？
根据满二叉树的节点规律，我们可以看到每一层的节点和层数是有如下的关系的：

0层：1
1层：2
3层：4
…
h-1层：2^(h-1)
根据等比数列求合公式，可得出，对满二叉树，h 层，一共有 2^h - 1 个节点，大约是 2^h，这里富裕一个节点，肯定可以放下 2^h - 1 个节点。
最后一层（h-1层），有 2^(h-1) 个节点。
可以看到，最后一层的节点数大致等于前面所有层节点之和。
有了上面的结论，如果区间有 n 个元素，用数组描述线段树需要有多少节点呢？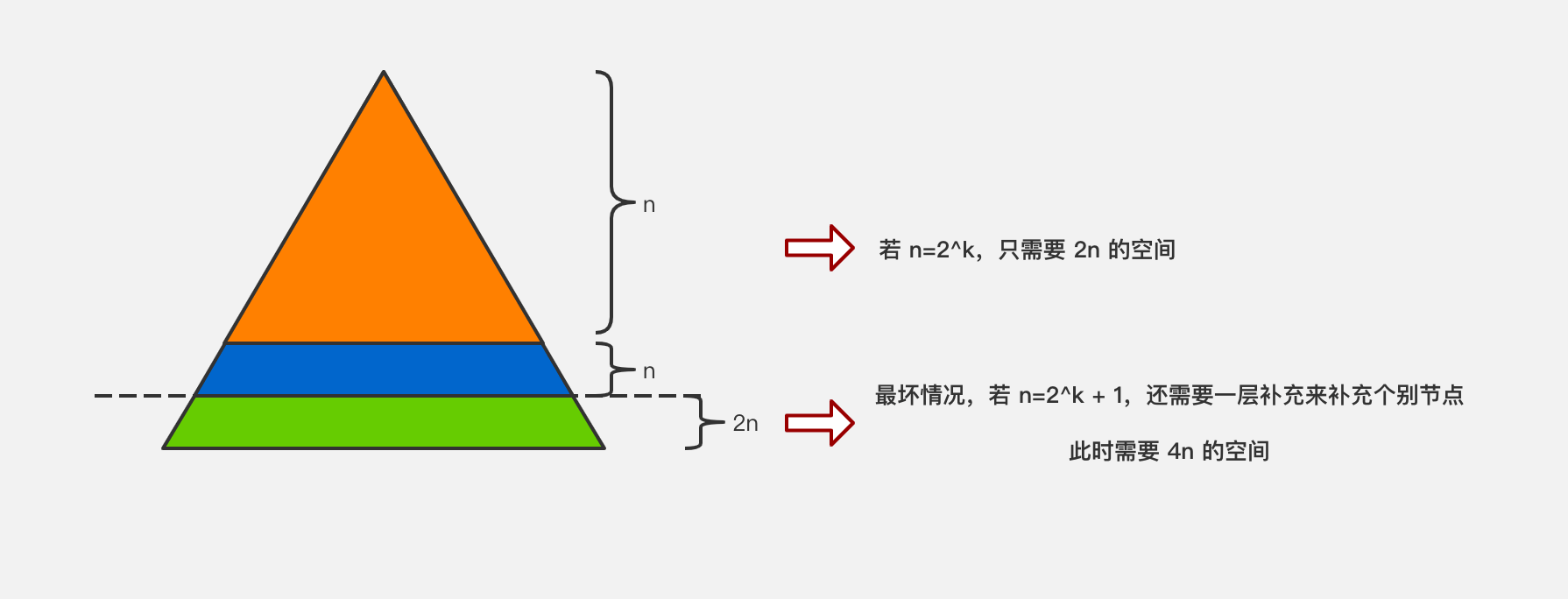

通过上面的推导，如果区间有 n 个元素，需要 4n 的空间来存储整个线段树。由于我们不考虑添加元素，即区间是固定的，所以使用 4n 的静态空间即可。

当然 4n 是一个估计值，这 4n 的空间并不是都被占满的，我们留有空余。比如下图的情况，最后一层大部分的节点是 null。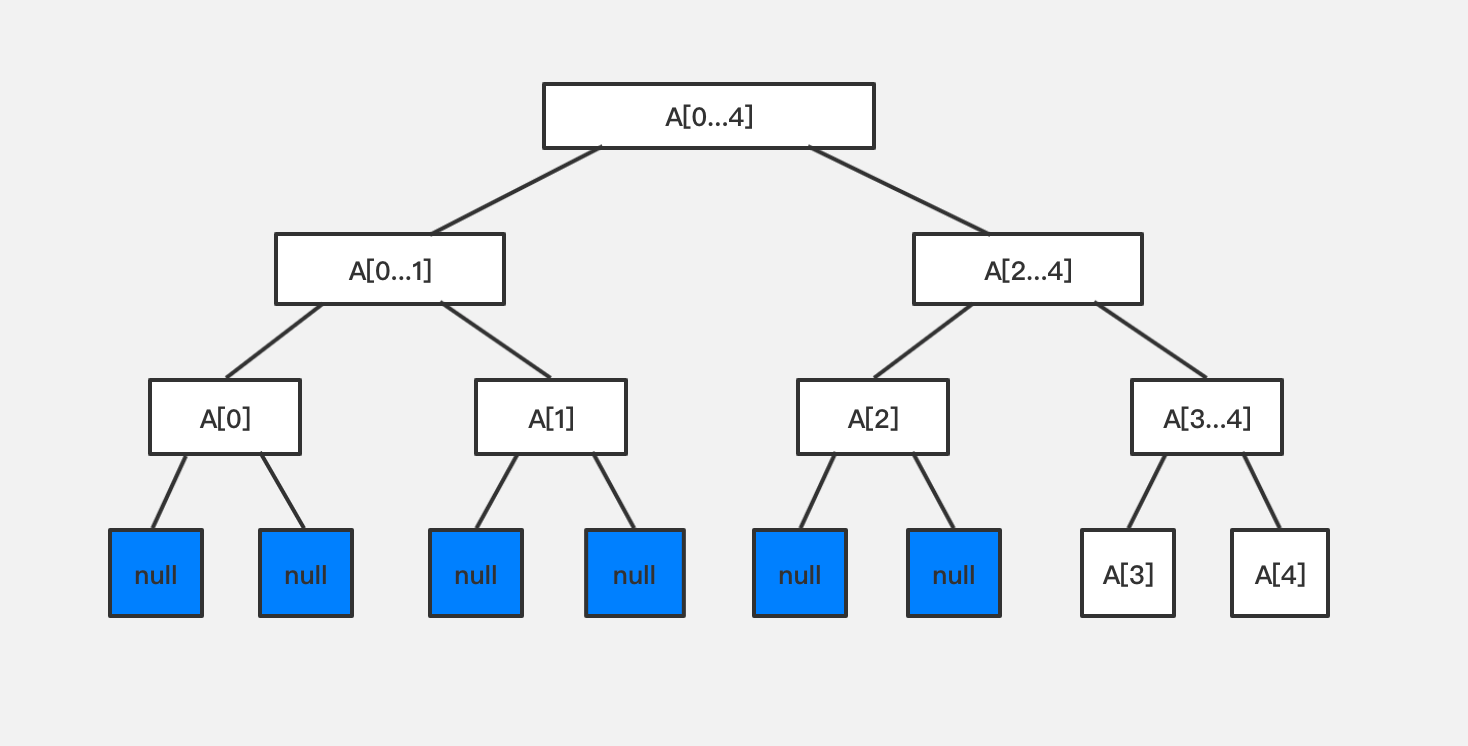

我们暂不考虑这种浪费的问题。对于现代计算机来说，多出来的这些节点基本是不影响空间的，这里就是算法的空间换时间的体现。

三、创建线段树

有了上面的分析，具体的代码实现其实很简单。data 是存储元素的数组，tree 是树结构使用的数组。

public class SegmentTree<E> {

    private Merger<E> merger;

    /**
     * 树结构 - 这里使用数组
     */
    private E[] tree;
    /**
     * 真正的数据
     */
    private E[] data;

    public SegmentTree(E[] arr, Merger<E> merger) {
        this.data = (E[]) new Object[arr.length];
        for (int i = 0; i < arr.length; i++) {
            data[i] = arr[i];
        }

        // 通过归纳，4倍的data长度用来创建线段树比较合适，可能会有空间的浪费，但是可以接受
        tree = (E[]) new Object[4 * arr.length];
        this.merger = merger;

        // 创建线段树
        buildSegmentTree(0, 0, arr.length - 1);
    }

    private void buildSegmentTree(int treeIndex, int l, int r) {
        ...
        ...
    }

    /**
     * 获取数据大小
     *
     * @return 数据大小
     */
    public int getSize() {
        return data.length;
    }

    /**
     * 根据索引获得数据
     *
     * @param index 索引值
     * @return 数据
     */
    public E get(int index) {
        if (index < 0 || index >= data.length) {
            throw new IllegalArgumentException("Index is illegal.");
        }
        return data[index];
    }

    /**
     * 返回一个索引表示的元素的左孩子的索引
     *
     * @param index 索引值
     * @return 左孩子的索引
     */
    public int leftChild(int index) {
        return 2 * index + 1;
    }

    /**
     * 返回一个索引表示的元素的右孩子的索引
     *
     * @param index 索引值
     * @return 右孩子的索引
     */
    public int rightChild(int index) {
        return 2 * index + 2;
    }

    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append("[");
        for (int i = 0; i < tree.length; i++) {
            if (tree[i] != null) {
                res.append(tree[i]);
            } else {
                res.append("null");
            }

            if (i != tree.length - 1) {
                res.append(", ");
            }
        }
        res.append("]");
        return res.toString();
    }
}

下面具体分析一下如何 build 线段树的节点。
我们利用树的递归结构来创建，treeIndex 表示正在创建的线段树的根节点的索引，l 表示区间的左边界，r 表示区间的右边界。递归终止的条件就是当左边界等于右边界（l == r）时，这时要构建的树 tree[treeIndex] 就是元素数组对应的索引的值（data[l] 或 data[r]）。之后找到当前线段树的左右子树的根节点索引和索引中间值 mid，接下来就是递归调用该方法，先创建左子树，后创建右子树，之后合并两棵子树得到正在创建的树的根节点数据。代码如下：

/**
     * 在 treeIndex 的位置创建表示区间[l...r]的线段树
     *
     * @param treeIndex 正在创建的线段树的根节点
     * @param l         表示区间的左边界
     * @param r         表示区间的右边界
     */
    private void buildSegmentTree(int treeIndex, int l, int r) {
        if (l == r) {
            tree[treeIndex] = data[l];
            return;
        }

        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);

        int mid = l + (r - l) / 2;
        buildSegmentTree(leftTreeIndex, l, mid);
        buildSegmentTree(rightTreeIndex, mid + 1, r);

        tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
    }

代码中的 merger 是对于合并这个操作的抽象，因为我们的线段树结构是一个通用的结构，不可能仅支持求合或求积的操作，这里就利用 java 的多态性，使用接口来抽象这个合并操作。具体的业务可以通过实现这个接口来实现自己的逻辑。

public interface Merger<E> {

    E merge(E a, E b);

}

以上，我们就完成了线段树的创建。
在下篇文章中，我们将看如何在线段树中进行查询和更新操作。