上篇我们认识了线段树，并创建了一棵线段树，这篇我们继续来看如何在线段树中查询和更新。

一、区间查询

我们创建线段树的时候，利用了树的天然递归特性，进行查询我们同样可以使用递归的思想。
定义一个 query 方法，queryL 参数表示查询区间的左边界，queryR 参数表示查询区间的右边界。首先考虑超出边界的异常情况，抛出相应异常。接下来就是我们核心的递归方法。
我们可以思考一下，定义这个递归函数，需要哪些必要的条件呢？

当前递归中正在处理的线段树

如何表示正在处理的线段树？指出当前树的根以及其左右边界即可。
- 正在处理的线段树的根节点索引（treeIndex）
- 正在处理的线段树的左边界（l）
- 正在处理的线段树的右边界（r）
我们最终需要查询的区间
- 区间查询左边界（queryL）
- 区间查询右边界（queryR）

所以我们的递归方法可以定义以上这 5 个参数。
定义好了方法，如何进行具体的查询操作呢？
首先考虑递归终止的条件，即我们正在处理的线段树的左边界等于需要查询的左边界，并且正在处理的线段树的右边界等于需要查询的右边界，此时，线段树中的节点 tree[treeIndex] 即为方法的结果。
接下来考虑递归的逻辑。和创建线段树一样，先找到当前处理树的中间节点索引和左右子树的索引。之后有以下几种情况：

查询左边界在中间节点索引 + 1的位置或还靠右，即 queryL >= mid + 1

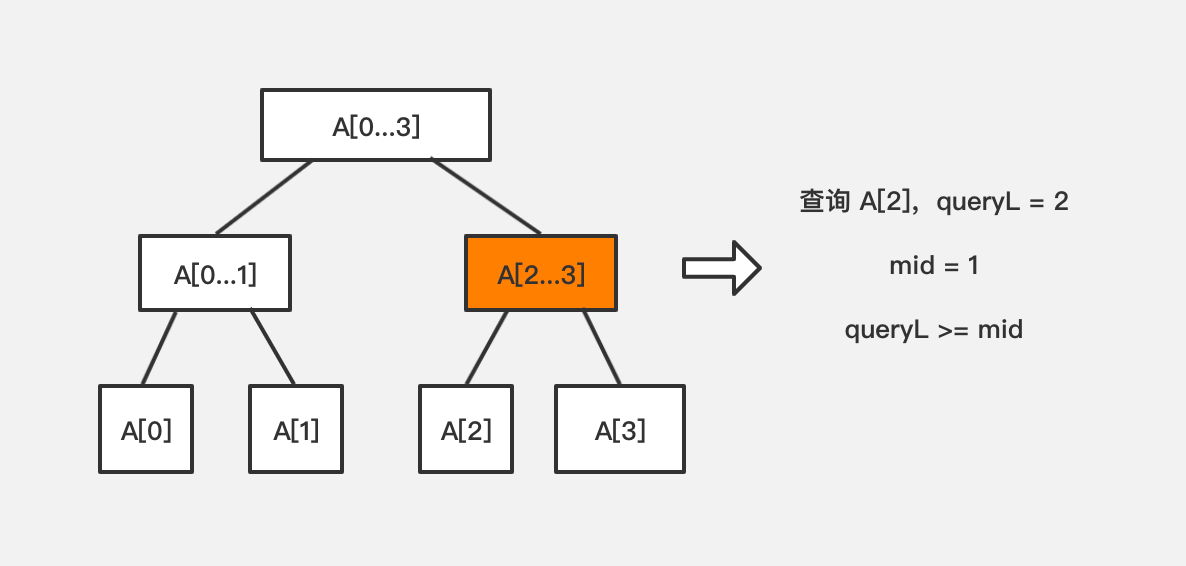
此时去右子树，从中间位置 mid + 1 到 r 的区间去查询 queryL 到 queryR
查询右边界在中间节点索引的位置或还靠左，即 queryR <= mid

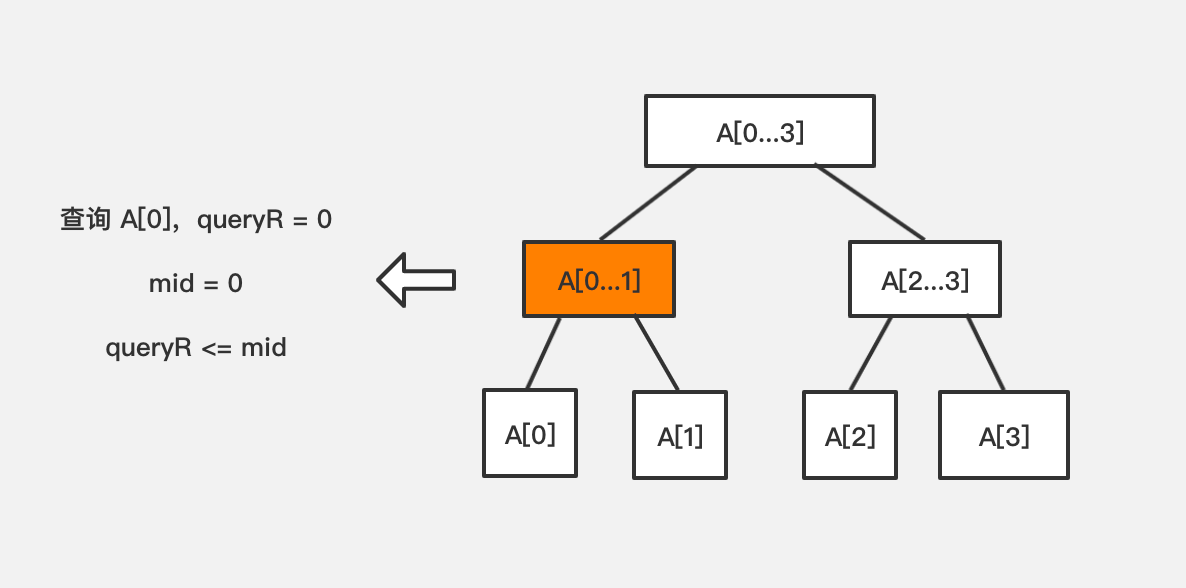
此时去左子树，从 l 到中间位置 mid 的区间去查询 queryL 到 queryR

查询的左右边界涉及左右子树的结果

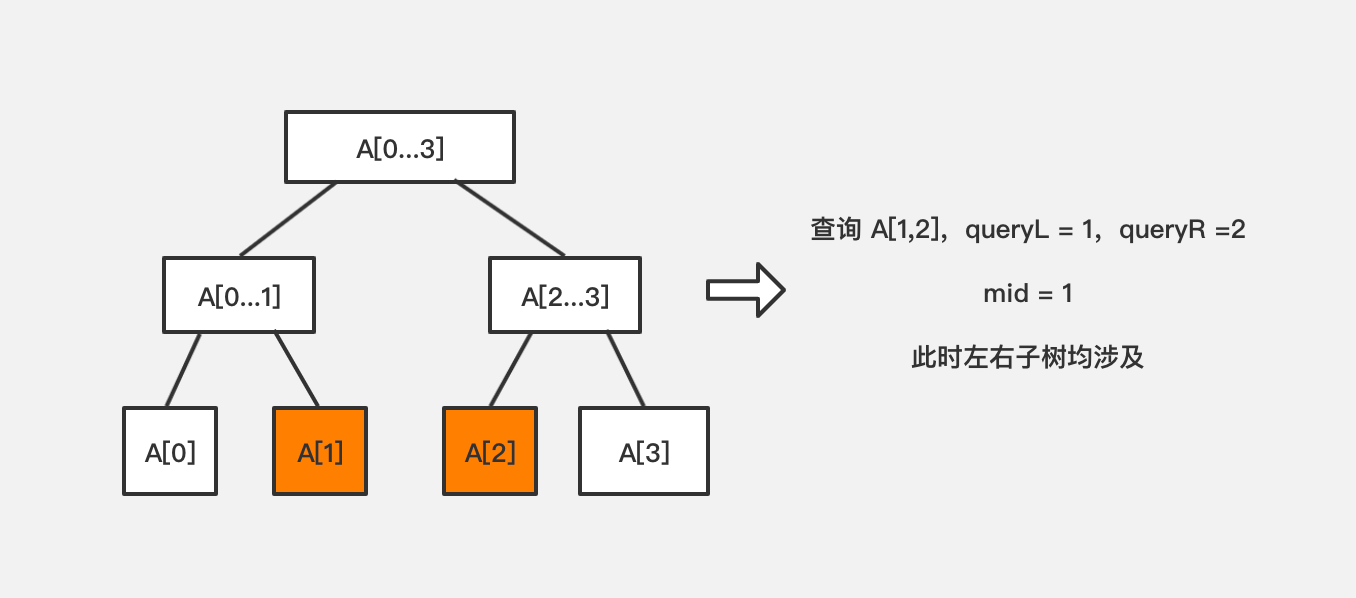
此时左右子树均涉及，需要在左子树查询 queryL 到 mid 区间，在右子树查询 mid + 1 到 queryR 区间，之后将左右结果聚合即可。

具体代码如下：

/**
     * 返回区间[queryL...queryR]的值
     *
     * @param queryL 左边界
     * @param queryR 右边界
     * @return 返回值
     */
    public E query(int queryL, int queryR) {
        if (queryL < 0 || queryL >= data.length || queryR < 0 || queryR >= data.length || queryL > queryR) {
            throw new IllegalArgumentException("Index is illegal.");
        }

        return query(0, 0, data.length - 1, queryL, queryR);
    }

    /**
     * 在以 treeIndex 为根的线段树[l...r]中的范围里，搜索区间[queryL...queryR]的值
     *
     * @param treeIndex 正在处理的树的根节点索引
     * @param l         正在处理的线段树的左边界
     * @param r         正在处理的线段树的右边界
     * @param queryL    查询左边界
     * @param queryR    查询右边界
     * @return 搜索到的值
     */
    private E query(int treeIndex, int l, int r, int queryL, int queryR) {
        if (l == queryL && r == queryR) {
            return tree[treeIndex];
        }

        int mid = l + (r - l) / 2;
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);

        if (queryL >= mid + 1) {
            return query(rightTreeIndex, mid + 1, r, queryL, queryR);
        } else if (queryR <= mid) {
            return query(leftTreeIndex, l, mid, queryL, queryR);
        }

        E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
        E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
        return merger.merge(leftResult, rightResult);
    }

二、区间更新

区间查询实现了，我们再来看看另一个重要的操作 - 区间更新。

区间更新，顾名思义，将某个索引位置的值更新之后，与之关联的区间都要有所更新，所以叫区间更新。
我们定义一个set方法，将索引位置 index 的值更新为 e。更新的思路其实很简单：

更新 data 数组相应索引的值
更新线段树 tree 数组相关联的节点值

更新 data 数组很简单，直接将 data[index] 赋值成 e 即可。
我们主要看一下如何更新 tree 数组的节点值。
由于更新某个位置的节点的同时，其父辈节点也要做出相应的改变，所以我们依然可以利用树的递归特性来更新。
定义一个递归方法，有了之前的经验，应该很好理解，直接看代码：

/**
 * 将 index 位置的节点更新成 e
 *
 * @param index 待更新节点的索引值
 * @param e     要更新成的值
 */
public void set(int index, E e) {
    if (index < 0 || index >= data.length) {
        throw new IllegalArgumentException("Index is illegal.");
    }
    //首先更新 data 对应索引的值
    data[index] = e;
    //更新 tree 数组（线段树）中所有关联的值
    set(0, 0, data.length - 1, index, e);
}

/**
 * 在以 treeIndex 为根的线段树中更新 index 的值为 e
 *
 * @param treeIndex 正在处理的线段树的根节点索引
 * @param l         左边界
 * @param r         右边界
 * @param index     待更新的索引值
 * @param e         要更新成的值
 */
private void set(int treeIndex, int l, int r, int index, E e) {
    if (l == r) {
        tree[treeIndex] = e;
        return;
    }

    int mid = l + (r - l) / 2;
    int leftTreeIndex = leftChild(treeIndex);
    int rightTreeIndex = rightChild(treeIndex);

    if (index >= mid + 1) {
        //index 比中间节点位置还靠右，去右子树操作
        set(rightTreeIndex, mid + 1, r, index, e);
    } else {
        //否则去左子树操作
        set(leftTreeIndex, l, mid, index, e);
    }
    //set过相应节点的值后不要忘记合并左右子树的结果，否则被操作的节点的父辈节点值将不会更新
    tree[treeIndex] = this.merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
}

这里需要特殊注意一点，在调用完左或右子树的 set 方法之后，一定不要忘记将调整后的左右子树的结果进行合并，并赋值给 tree[treeIndex]，否则被更新的节点的父辈节点将不会进行更新。

到此，线段树的区间查询和区间更新我们都实现了。

三、相关问题

我们建立好了线段树的数据结构，就可以利用线段树来解决相应的问题。
比如上一篇文章中提到的，查询2019年注册用户里截至目前消费额最高的用户，这里我们可以将用户消费额信息包装成对象，当做线段树中的节点，data 的长度就是所有用户的数量，创建线段树，merger 实现这里是选出消费额最大值。伴随用户消费额的改变，使用区间更新的操作更新线段树相应节点的值（时间复杂度 O(logn)），比从头到尾遍历的更新（时间复杂度 O(n)）效率更高。
当然这里只是一个思路，具体实现会有更加细节的考虑。

思考

如何对一个区间进行更新
比如将区间 [2,5] 中所有元素 +5。

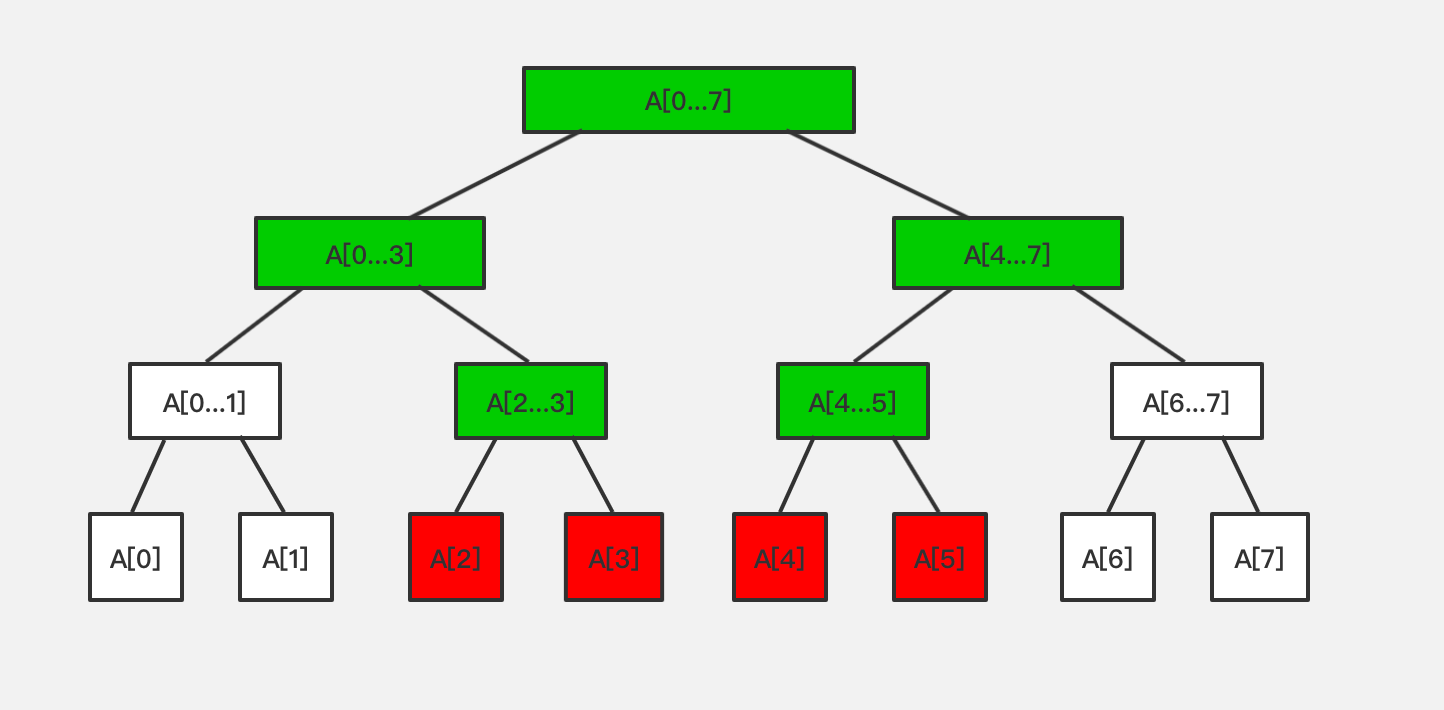
首先可以通过 O(logn) 的时间复杂度找到 A[2…3] 和 A[4…5] 这两个节点，以求和业务为例，这两个节点都包含2个元素，每个元素都需要 +5，所以这两个节点每个都要加 5*2=10 ，在回溯回去的时候，相应的这两个节点的祖辈节点也需要进行更新。需要注意，我们不能只更新中间节点（即涉及到的非叶子节点），图中红色标识的节点其实是要做 +5 操作的，如果我们对这些叶子节点同时也进行更新的话，其实我们进行了一次 O(n) 复杂度的操作，这个操作相对来说是比较慢的。
此时我们其实可以先不更新叶子节点的值，先使用一个数组 lazy 来记录未更新的内容，有了这个记录我们就不需要实际地去更新这些节点，当我们再有一次更新或查询操作再次碰到这些节点的时候，根据 lazy 记录判断，是否有需要更新的内容未更新，先更新之后再进行之后的操作，这种操作是一种懒惰更新的思想。这样以来，我们对于更新一个区间的操作，时间复杂度又变成了 O(logn)
数据量如此大的情况，我们是否还需要按照上面的方式创建 4n 大小的空间
这样浪费的空间就会很多，出于这个考虑，我们能否将上面的结构改用链式存储？
比如给定一个区间 [0,100000000]，而我们需要关注 [15,20] 区间的数据，此时如果建立 4n 的空间，将是浪费了很多很多空间，这时候我们可以根据需要动态地进行构建线段树。大体思路如下图：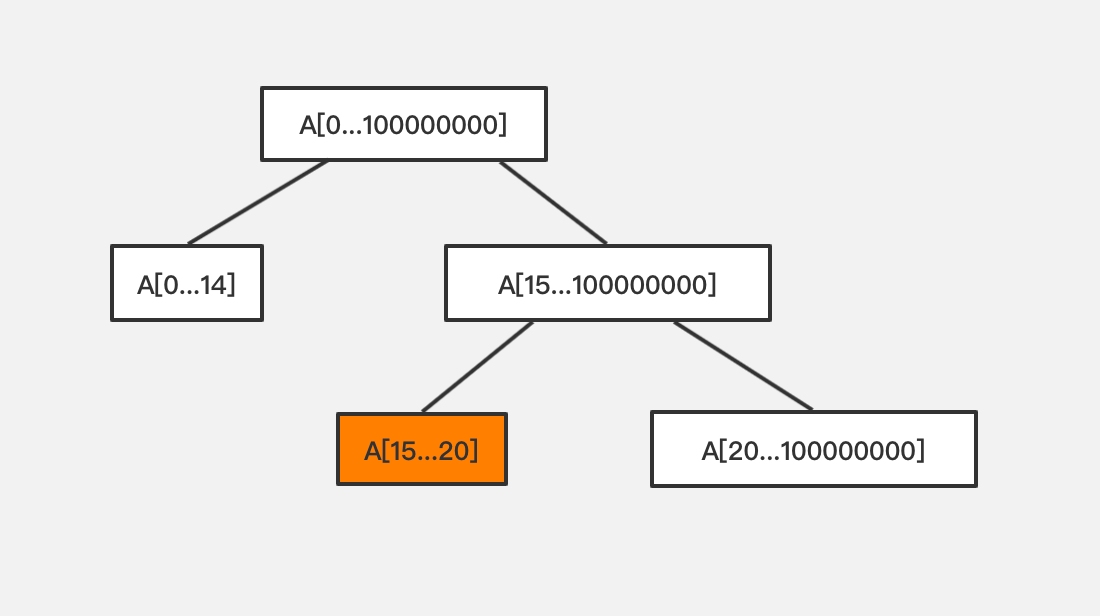

根据关注区间，分段创建线段树，这样节省了很多空间而且也减少了一些无用的递归操作。

关于线段树我们先讨论这么多，主要知道线段树能够解决哪些问题和背后的一些思想。当然线段树也是一种比较高级的数据结构，能够探索的地方还有很多很多，我们只是讨论了一些基础的定义和思想。能够把这些看似基础抽象的数据结构与实际应用关联，其实也是很有意思的事情。