很久没有更新文章了,周末又巩固了一下数据结构基础,这次我们来看一下有些不一样的树结构-并查集。
一、什么是并查集
下图所示的一些节点,节点之间可以相连,如果想要知道某两个节点是否可以连通,这个问题如何解呢?
这是典型的连接问题,像下图这种节点很少的情况,肉眼一看就会得到答案,但当有成千上万的节点时,又该如何解决问题呢?我们要说的并查集就是解决连接问题的一种解决方案。
并查集可以非常快速地判断网络中节点的连接状态。这里的网络是一个抽象的概念,比如可以是社交网络,那么人就是一个一个的节点,人与人之间的关系就是节点与节点之间的边,若要知道两个人之间是否有直接或间接的好友关系,就可以使用并查集来实现。
对于一组数据,并查集主要支持两个动作:
union(p,q)
在并查集内部,将p、q两个元素以及他们所在的集合合并起来。isConnected(p,q)
查询对于给定的两个数据p、q,他们是否属于同一个集合。
对于并查集的这两个动作,我们可以抽象出一个接口来表示。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33/**
* UnionFind并查集接口
*
* @author renxiaoya
* @date 2020-12-06
**/
public interface UF {
/**
* 获取并查集中有多少元素
*
* @return 并查集中有多少元素
*/
int getSize();
/**
* 两个元素是否相连
*
* @param p 元素编号p
* @param q 元素编号q
* @return 是否相连
*/
boolean isConnected(int p, int q);
/**
* 将两个元素并在一起
*
* @param p 元素编号p
* @param q 元素编号q
*/
void unionElement(int p, int q);
}
这里我们的p和q指的是一个抽象的编号,可以理解为索引编号,比如isConnected(p,q)代表了编号为p的元素和编号为q的元素是否相连,至于p、q元素到底指的是什么,我们并不关心。接下来,我们来看看如何实现这个接口,实现并查集的功能。
二、并查集的实现
假设有10个元素,编号从0到9,当然这些节点都是业务的抽象,可以是10个人、10辆车、10本书等等,具体的含义与不同的业务逻辑有关。在并查集的内部,我们只存这10个编号,表示具体的10个元素,每一个节点所存储的是它所属的这个集合的id。下图中,元素0所属的集合id为0,元素1所属的集合id为1,元素2所属的集合id为0,以此类推。不同的id值可以理解为不同的集合所对应的编号。下图的例子可以看成是把10个元素分成了两个集合,其中0,2,3,6,7,9这几个元素在一个集合中1,4,5,8这几个元素在另外的一个集合中。其实可以很容易的想到,我们可以使用一个数组来存储这样的结构,数组的索引就是对应的元素编号,索引所对应数组中的值就是集合的id。图中的元素0和元素2所对应的id值都为0,可以说元素0和元素2可以相连接。
Quick Find
上面说到并查集主要的两个操作union(p,q)和isConnected(p,q),对于数组存储的并查集来说,可以很容易的回答isConnected(p,q),只需要看,数组索引p、q对应的值是否相同即可。这里我们把找到数组索引p或者q对应值的过程,也抽象为一个方法find(p)。那么判断isConnected(p,q)就转化为了判断find(p)与find(q)是否相等。

很显然,以上操作的时间复杂度是O(1),对于这种存储的并查集,find这个操作是非常快的。
上面介绍了find的思路,接下来我们来看一下并查集另一个重要的动作union(p,q),我们可以称为Quick Union。
还是以上面的并查集为例,如果想要实现union(1,2),就需要把元素1所在集合与元素2所在集合合并起来,也就是说,这两个集合合并之后,集合中每一个元素对应的集合id值都是相同的。我们可以把元素1所在集合合并到元素2所在集合,也可以把元素2所在集合合并到元素1所在集合,要么全是0,要么全是1。
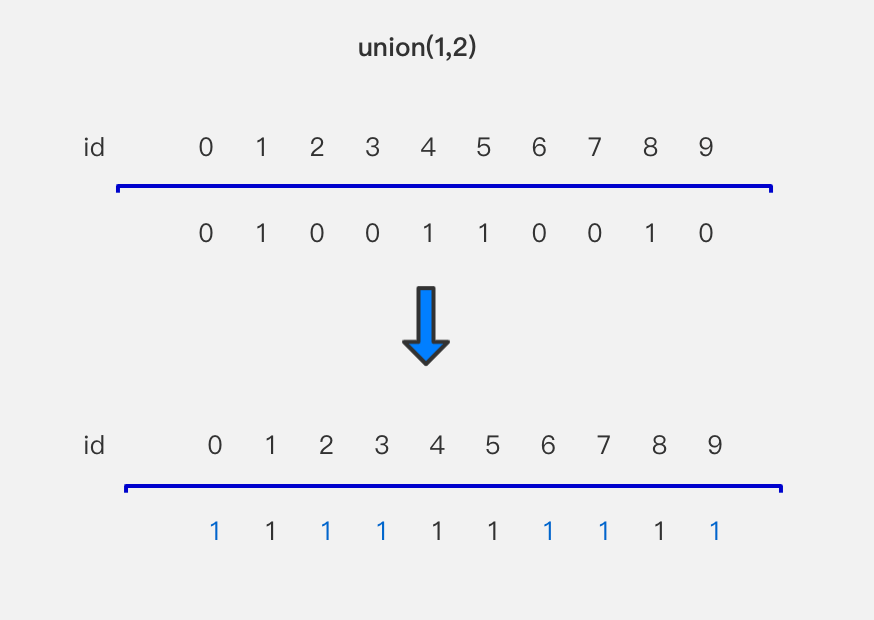
实现思路也很简单,先找到元素p、q对应的id,如果id已经是相等的,说明元素p、q已经在一个集合中,直接return即可;否则的话,遍历一遍当前数组,每次遍历,如果当前索引下标对应的值与元素p对应的id相等,此时将当前索引下标对应的值设置为元素q对应的id。
因为遍历了一遍数组元素,所以union(p,q)的时间复杂度是O(n)。
因为find操作时间复杂度是O(1),而union的时间复杂度是O(n),所以这样实现的并查集我们也称为是Quick Find
思路清楚了,下面我们看看代码如何实现Quick Find的并查集。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65/**
* 并查集实现 - v1
* <p>
* 0 1 2 3 4 5 6 7 8 9
* -------------------
* 0 1 0 1 0 1 0 1 0 1
* <p>
* OP | 时间复杂度
* unionElement(p,q) --> O(n)
* isConnected(p,q) --> O(1)
*
* @author renxiaoya
* @date 2020-12-06
**/
public class UnionFind1 implements UF {
private int[] id;
public UnionFind1(int size) {
id = new int[size];
for (int i = 0; i < id.length; i++) {
id[i] = i;
}
}
public int getSize() {
return id.length;
}
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
public void unionElement(int p, int q) {
int pId = find(p);
int qId = find(q);
if (pId == qId) {
return;
}
for (int i = 0; i < id.length; i++) {
if (id[i] == pId) {
id[i] = qId;
}
}
}
/**
* 查找元素p对应的集合编号
*
* @param p 元素p
* @return 集合编号
*/
private int find(int p) {
if (p < 0 || p >= id.length) {
throw new IllegalArgumentException("p is out of bound.");
}
return id[p];
}
}
以上,我们实现了Quick Find的并查集。既然有Quick Find,是否有Quick Union呢?答案是肯定的。接下来我们来看一看如改进上面的实现,来提高union操作的效率。
Quick Union
上面实现的Quick Find好像和树没有任何关系,不要着急,我们来看看Quick Union的实现思路。
我们把每一个元素都看作是一个节点,节点之间相连接,形成了一个树的结构。不过这里的树和之前实现的二叉树、trie等是不同的,在并查集中实现的树结构是孩子指向父亲的。
看个简单的示例。节点3与节点2相连接,其实就是节点3指向了节点2,而这里节点2是树的根节点,对于节点2,它指向自己。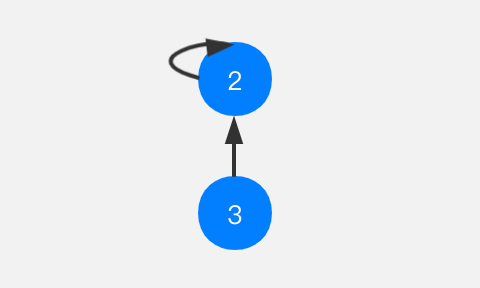
如果节点1想要和节点3合并,就把节点1指向节点3所在树的根节点,也就是节点2。
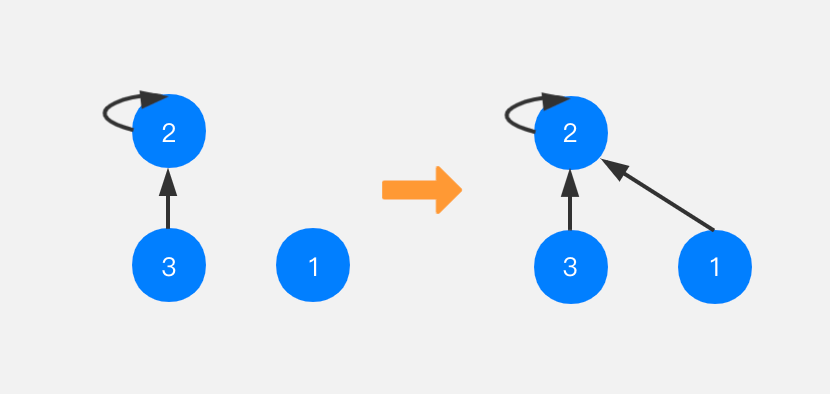
如果并查集中有一棵树是左边子树的样子,5和6节点指向7节点,此时想要将节点7与节点2进行合并,如何操作呢?实际上是将节点7所在树的根节点指向节点2即可。
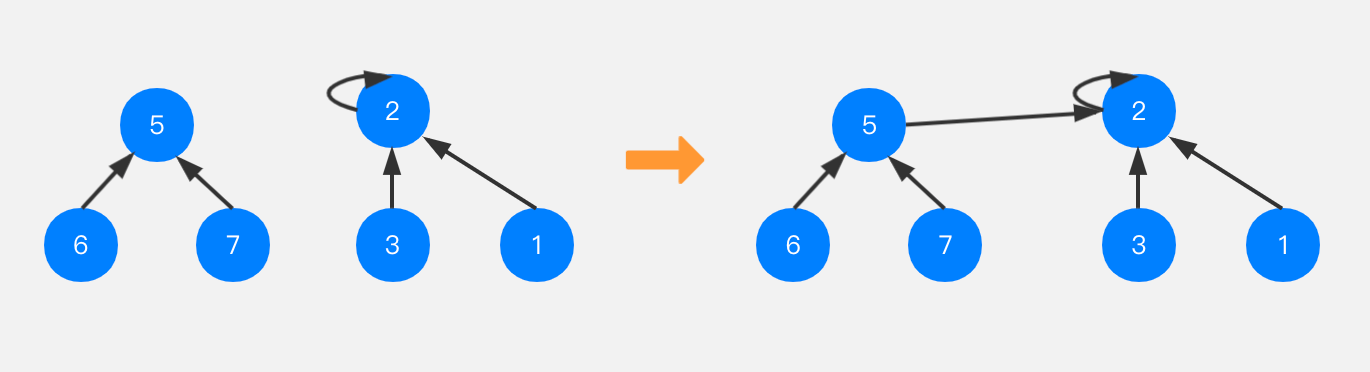
如果我们想将节点7与节点3合并,得到的结果还是上图的样子,其实合并操作是将节点7所在树的根节点指向节点3所在树的根节点,也就是节点2。
以上就是真正并查集实现的思路,和上面Quick Find实现的存储发生了变化,实际上也是很简单的。通过观察,我们发现针对每一个节点,只有一个指针,只会指向另一个元素,对于这个指针的存储,我们依然可以使用数组的方式来存储。这个数组,我们可以叫作parent,parent[i]表示的就是第i个元素所在的节点指向了哪个元素。
在初始化的时候,每一个节点都没有和任何一个节点合并,都指向了自己,也就是parent[i]都等于i。
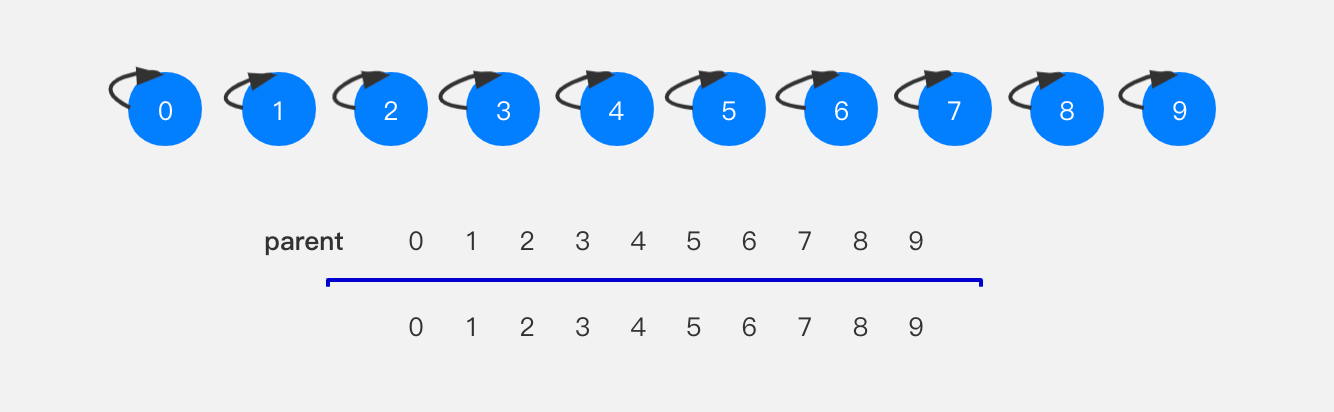
当要执行union(4,3)时,将节点4指向节点3,对应parent数组,就是将parent[4]设置为parent[3]的值。
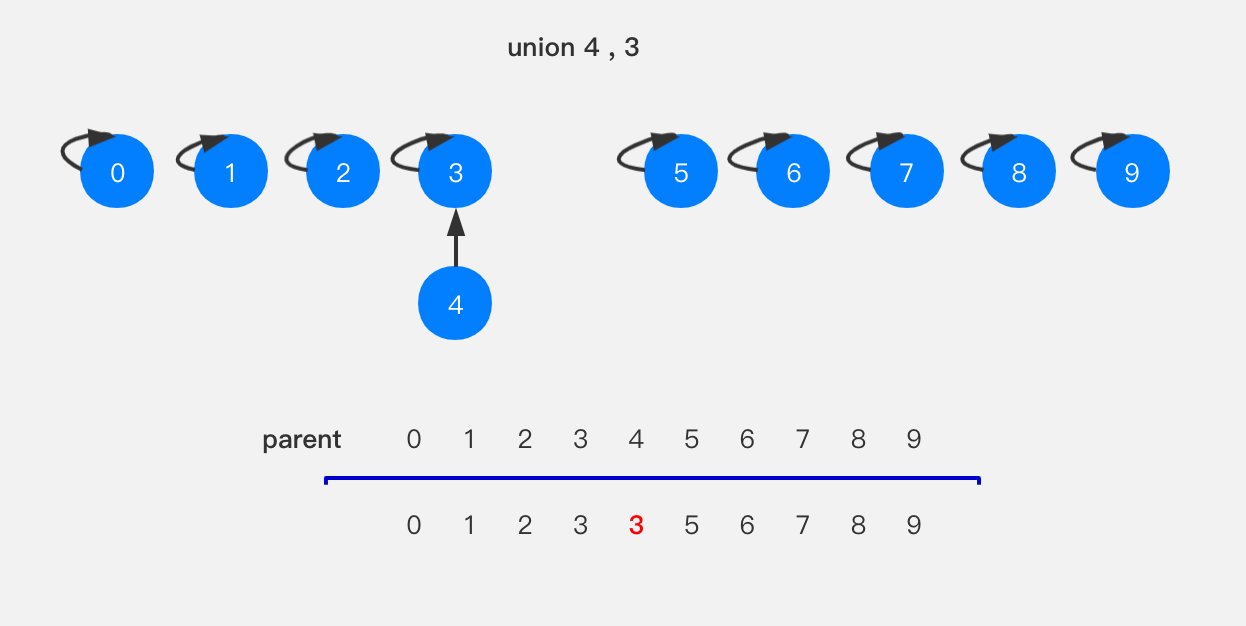
要执行union(3,8),就是将节点3所在的树指向节点8,相应的parent[3]设置为8;执行union(6,5),就是将节点6指向节点5,parent[6]设置为5。
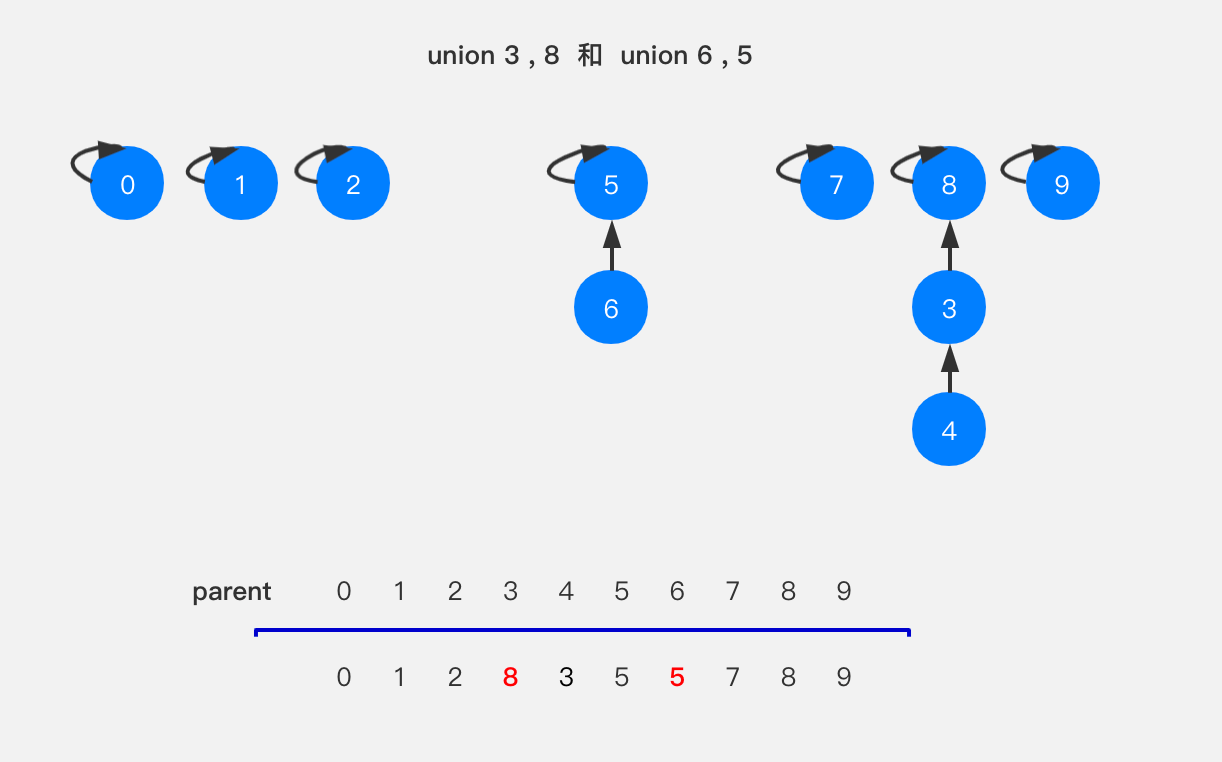
执行union(9,4),就是将节点9指向节点4所在这棵树的根节点,这里涉及到了一个查询操作,查询节点4所在的根节点,我们先看节点4的父节点是3,不是4本身,继续查找节点3的父节点为节点8,也不是节点3本身,说明还不是这棵树的根节点,我们继续往下找,看节点8的父节点是8,与节点8本身相等,说明这是个根节点,此时我们便找到了节点4所在这棵树的根节点,也就是节点8。
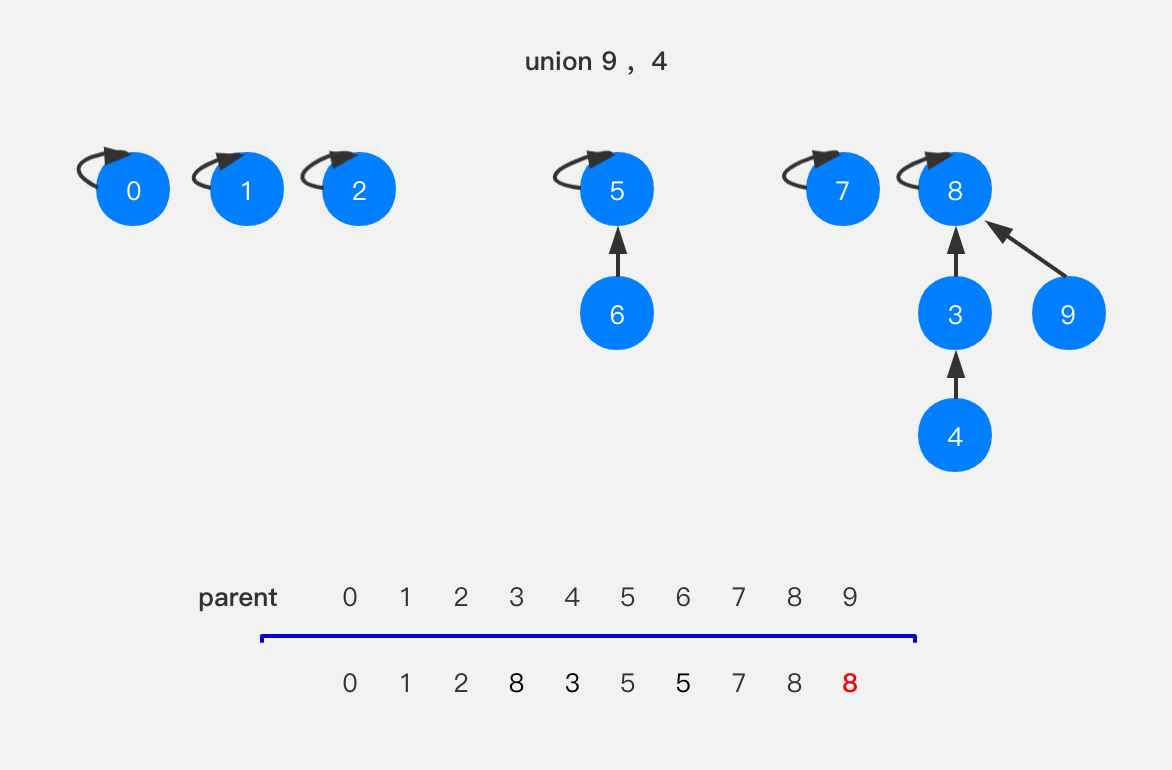
上图中可以看到,节点9指向了节点8,我们为什么不直接指向节点4呢?很显然,指向节点4的话就形成了一个链表,之后如果再进行查找节点9所在树的根节点时,就等同于遍历了这个链表,树的优势就体现不出来了;而指向节点8时,当查找节点9所在树的根节点时,我们向上查1次就能得到结果。所以在数组中,parent[9]设置成8。
按照上面的规律,我们执行union(2,1)和union(5,0),可以得到下图的结果。
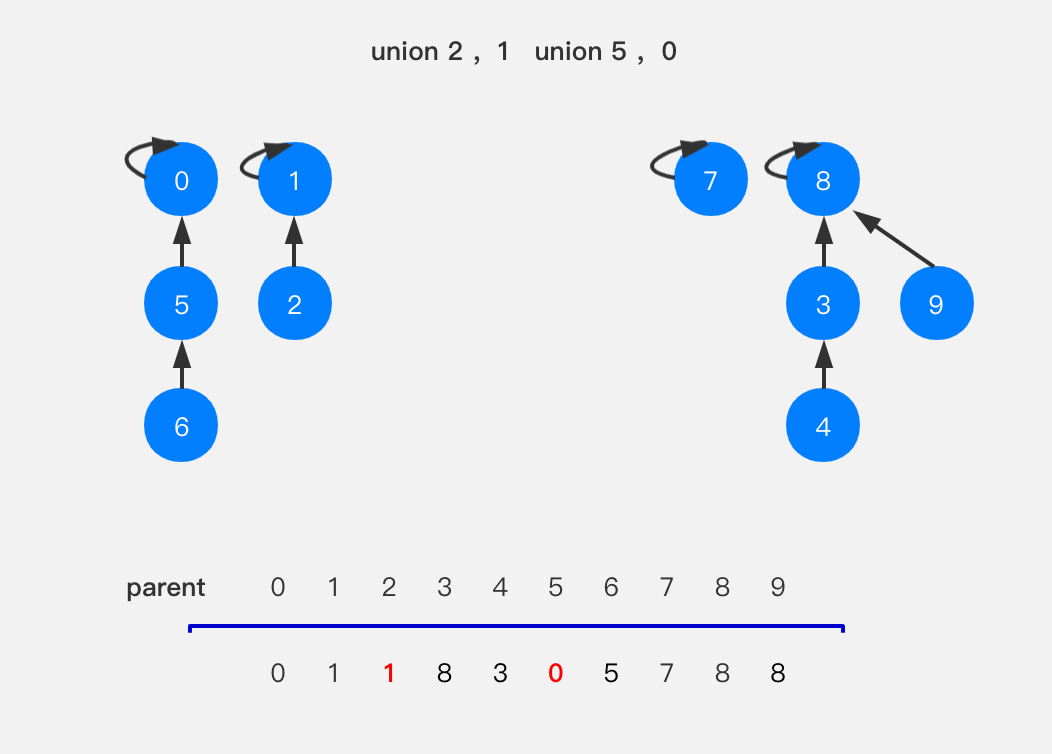
执行union(7,2)和union(6,2),前者很简单,无需多说,后者稍微复杂一些,我们要找到节点6所在树的根节点,让它指向节点2所在树的根节点,也就是节点0指向节点1。

以上的操作,是并查集通常的实现。通过分析,我们知道这种union操作的时间复杂度是O(h),h表示的是union的两个元素所在树深度的大小,通常这个深度的大小比元素的个数要小的多,所以这个union的过程相对来说会快一些;不过相应的代价就是查询操作,如果我们想知道节点5和节点4是否相连,我们要找到节点5和节点4对应的根节点,比较两个根节点是否相等,这里节点5的根节点是1,节点4的根节点是8,1和8不相等,所以节点5和节点4不是相连的,这一查找的过程时间复杂度也是O(h)。我们通过牺牲了查询操作的性能提升了合并操作的性能,不过通常情况下,树的深度是远远小于元素的总数的,所以我们让查询和合并都是树的高度这个时间复杂度,在大多数情况下,性能是可以接受的。
知道了查找和合并的思路,下面我们来看看代码实现。
1 | /** |
三、可以再优化吗
上面我们实现了两种并查集,这两种实现的性能如何呢?我们来测试一下。
对于size=10000,进行10000次合并和10000次查询操作。具体测试代码这里就不贴出来了,来看结果吧。对比之下:1
2
3
4UnionFind1 : 0.05409653s
UnionFind2 : 0.035575485s
Process finished with exit code 0
上面结果差异并不明显,我们增加size,对于size=100000,进行10000次合并和10000次查询,结果变成了如下的情况:
1 | UnionFind1 : 0.269145621s |
如果我们把操作次数也设为100000,又会变成什么样呢?1
2
3
4UnionFind1 : 5.205210688s
UnionFind2 : 10.711065036s
Process finished with exit code 0
对于v1版本的并查集,我们就是使用数组的顺序遍历,是对一片连续的空间进行了一次循环的操作,这样的操作,jvm有很好的优化,所以运行速度会非常快。
而对于v2版本的并查集来说,这个查询的过程其实是一个不断索引的过程,它不是一个顺次访问一片连续空间的过程,要在不同的地址空间进行跳转,因此速度会相对慢一些;再者,v2的并查集,find和union的复杂度都是O(h),我们增大了操作数,意味着在union的过程中,将更多的元素都组织在了一个集合中,这棵树就变得非常庞大,深度也有可能会非常高,导致我们进行这100000次操作的时候,isConnected消耗的时间也会比较多。所以这次的测试结果,v2版本的效率显得更慢一些。
针对size的优化
其实对于v2版本的并查集,我们有很大的优化空间,我们回忆一下,在进行union操作的时候,是没有考虑树的特点就进行合并指向的,我们来看下面的过程。
依次进行union(0,1),union(0,2),union(0,3)操作,我们的并查集变成了这个样子。
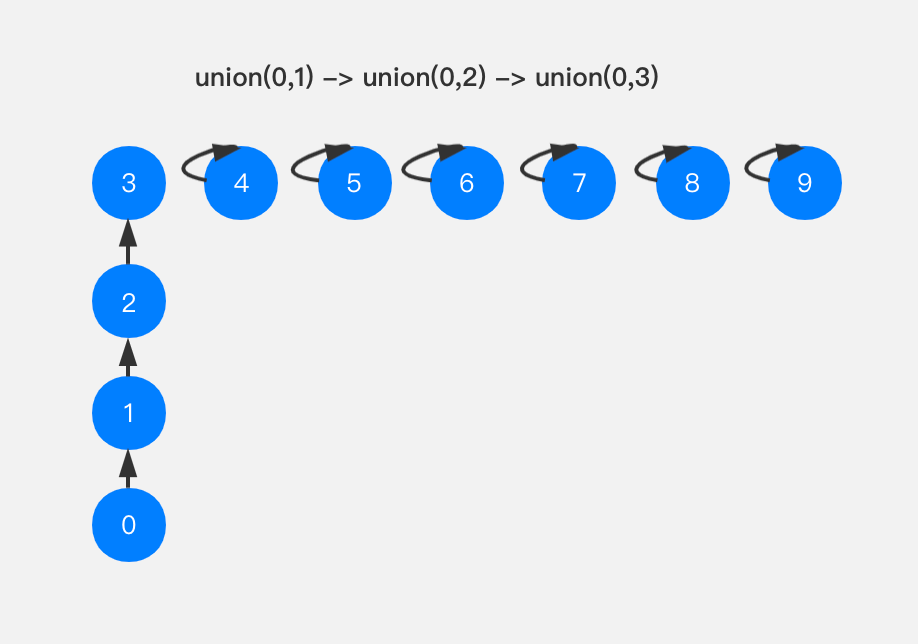
很明显,这样已经形成了一个链表,当我们继续进行union(0,n),最终我们的并查集实际上就是一条长长的链表了。这种情况我们如何进行优化呢?
一个简单的思路,我们考虑当前节点所在的这棵树的节点多少,将节点少的这棵树合并到节点多的树上,就可以有效的降低树的高度。比如上述例子,我们进行union(0,3)时,比较一下节点0所在树的size(3)和节点3所在树的size(1),将size小的向size大的树合并,即将节点3指向节点2。
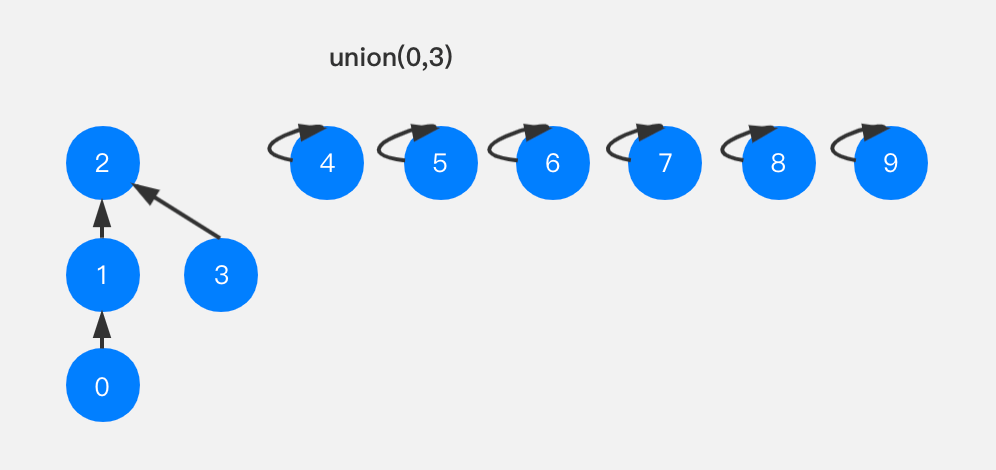
这样我们可以有效地降低树的高度。代码改造如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71/**
* 并查集实现 - v3
* 与v2相比,优化了size,unionElement时,将节点数少的树指向节点数多的树
*
* @author renxiaoya
* @date 2020-12-06
**/
public class UnionFind3 implements UF {
private int[] parent;
/**
* sz[i]表示以i为根的集合中元素的个数
*/
private int[] sz;
public UnionFind3(int size) {
parent = new int[size];
sz = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
sz[i] = 1;
}
}
public int getSize() {
return parent.length;
}
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
public void unionElement(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
// 若pRoot所在元素比qRoot所在元素少,将pRoot指向qRoot,并维护sz
if (sz[pRoot] < sz[qRoot]) {
parent[pRoot] = qRoot;
sz[qRoot] += sz[pRoot];
} else {
// 否则将qRoot指向pRoot
parent[qRoot] = pRoot;
sz[pRoot] += sz[qRoot];
}
}
/**
* 查找元素p对应的集合编号
*
* @param p 元素p
* @return p对应的元素编号
*/
private int find(int p) {
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
while (p != parent[p]) {
p = parent[p];
}
return p;
}
}
现在我们再来看看在size=100000,操作数也为100000的测试用例中,并查集的表现。1
2
3
4
5UnionFind1 : 5.266835514s
UnionFind2 : 11.177287476s
UnionFind3 : 0.021229747s
Process finished with exit code 0
优化的效果是非常明显的,v3版本的并查集仅用了0.02秒就完成了操作。
基于rank的优化
上面基于size的优化,我们考虑了树所在的节点个数多少来降低树的高度,那何不更直接的来比较树的高度呢?
假设有如下的并查集,需要进行union(4,2)操作。
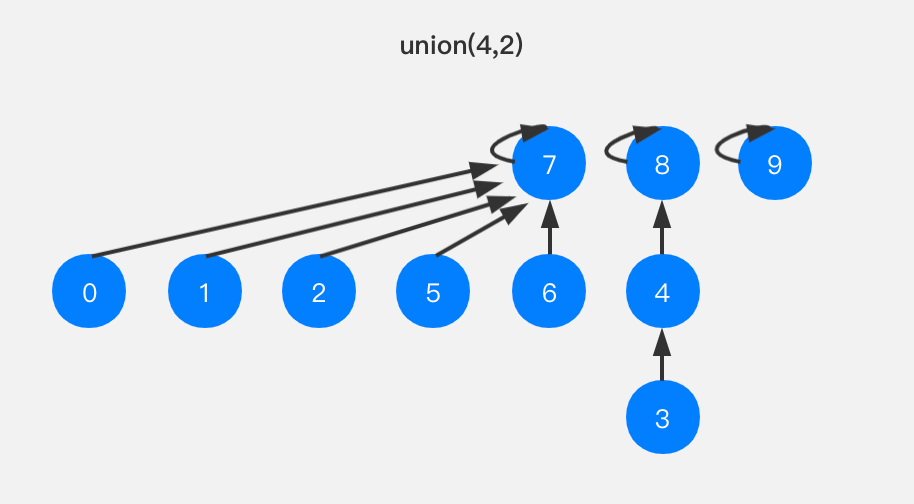
若按照size优化的思路,我们会将节点8指向节点7,因为节点4所在树的size比节点2所在树的size小,如下图所示:
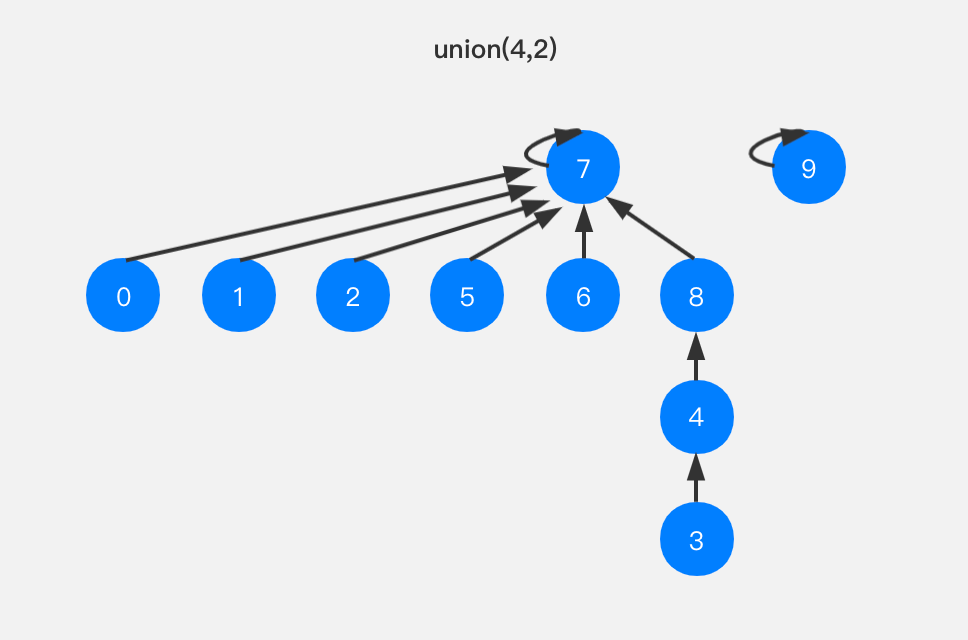
这样树的高度是4。如果我们直接来比较树的高度来进行合并呢?将高度低的向高度高的树合并,如下图所示:
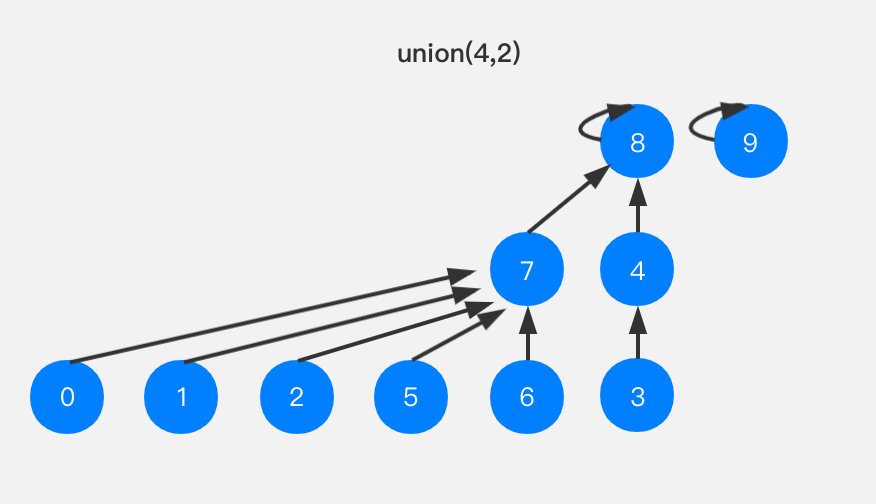
这样树的高度是3,比基于size的优化得到的树的高度更低。
我们来看看代码如何实现,其实与size优化的代码很像,只是用一个int数组代表了以i为根的树的高度,合并的时候判断高度,将高度低的向高度高的树合并,并在合适的时候维护rank的值即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75/**
* 并查集实现 - v4
* 针对rank优化,unionElement时,深度低的树指向深度高的树
* 这里是rank,排名、序的意思,不是绝对的高度
*
* @author renxiaoya
* @date 2020-12-06
**/
public class UnionFind4 implements UF {
private int[] parent;
/**
* rank[i]表示以i为根的集合中元素的高度rank
*/
private int[] rank;
public UnionFind4(int size) {
parent = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
rank[i] = 1;
}
}
public int getSize() {
return parent.length;
}
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
public void unionElement(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
// 根据两个元素所在的树的rank不同判断合并的方向
// 将rank低的集合指向rank高的集合
if (rank[pRoot] < rank[qRoot]) {
parent[pRoot] = qRoot;
} else if (rank[qRoot] < rank[pRoot]) {
parent[qRoot] = pRoot;
} else {
// rank[qRoot] == rank[pRoot]
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}
}
/**
* 查找元素p对应的集合编号
*
* @param p 元素p
* @return p对应的元素编号
*/
private int find(int p) {
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
while (p != parent[p]) {
p = parent[p];
}
return p;
}
}
我们来测试一下基于rank的优化结果吧。由于前两种并查集实现的效率很低,这里就不进行测试了,我们来比较v3和v4的效率。
我们增大数据量,拿size=10000000,操作数也为10000000来进行测试,结果如下:1
2
3
4UnionFind3 : 4.168454361s
UnionFind4 : 4.285047797s
Process finished with exit code 0
可以看到实际上基于size和基于rank的优化的结果是差不多的,只不过基于rank的优化在思路上更加顺一些,所以通常实现的并查集也使用基于rank的优化方案。
路径压缩
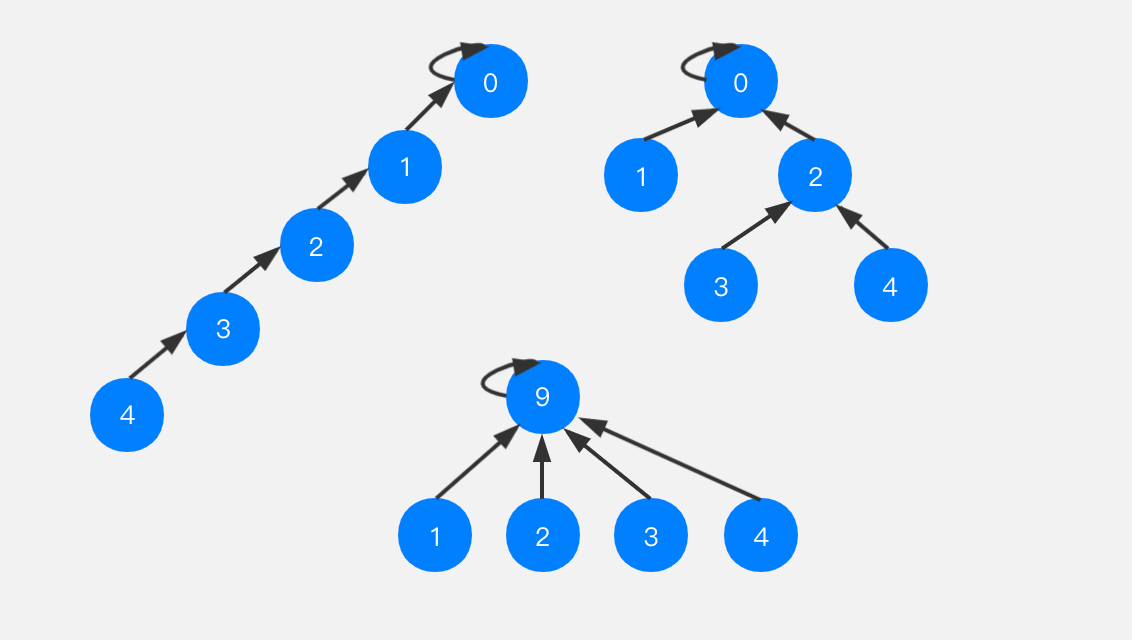
有如下图的情况,这三种都可以表示并查集中相连的一些节点。我们执行isConnected来查询任意两个节点,都可以得到相同的结果,但是很显然,这些树的深度不同,对应的效率也是区别的。比如最左侧的树,高度达到了5,那么在进行find(4)的时候需要花费的时间就会比较长;而下面的这棵树,高度只有2,那么进行find(4)的操作速度就会很快。
在我们上面实现的并查集中,进行union的过程,免不了会使树的高度越来越高,路径压缩就是可以将一棵树可以压缩成比较矮的树
我们在进行find操作的时候,会依次向上查询根节点,如果在向上查询的过程中,我们同时进行路径压缩,是否可以降低树的高度呢?
下图中的并查集,我们进行find(4)操作。
如果当前节点不是根节点,那么我们执行parent[i] = parent[parent[i]]操作,即将当前节点的父节点,指向父节点的父节点,文字描述比较绕,看图就比较清晰了。
节点4不是根节点,将节点4的父节点指向其父节点也就是节点3的父节点–节点2。
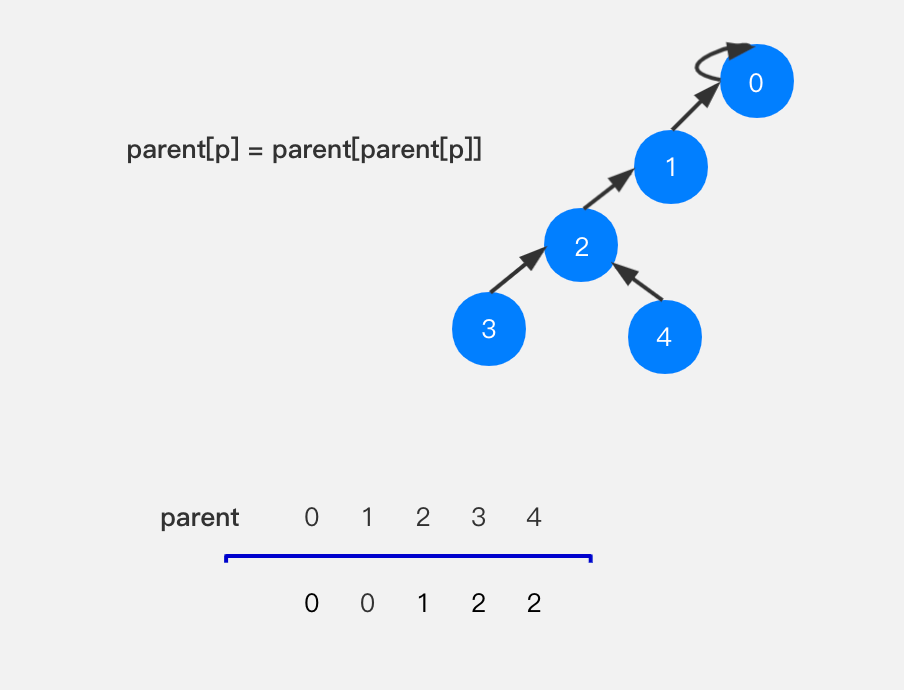
节点2不是根节点,将节点2的父节点指向其父节点也就是节点1的父节点–节点0。
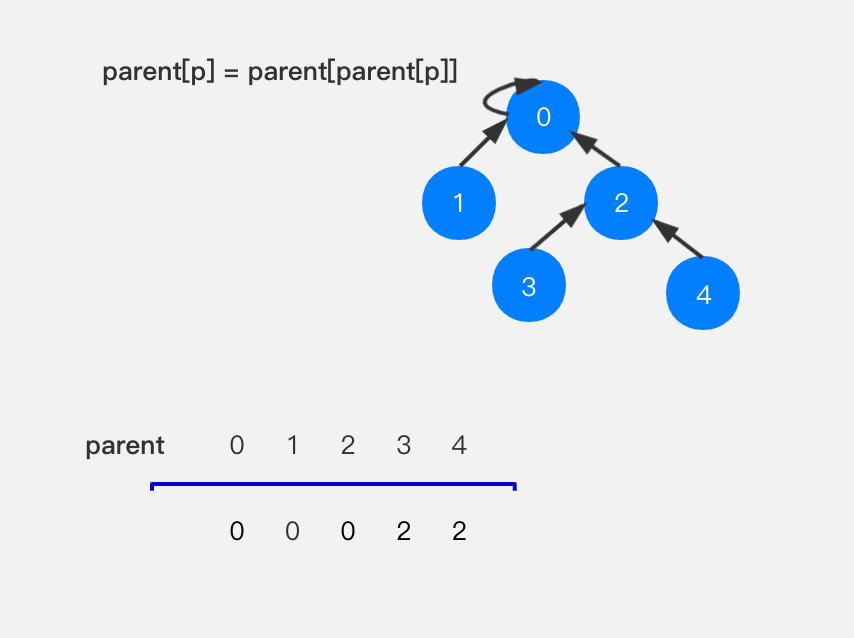
经过上述的操作,就将高度为5的树压缩成了高度为3,完成了一次路径压缩。
代码也是很简单的,在基于rank优化的代码中,我们改造find方法,判断节点p是否是根节点,不是的话就执行parent[i] = parent[parent[i]]。1
2
3
4
5
6
7
8
9
10private int find(int p) {
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
while (p != parent[p]) {
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
我们用同样的测试用例再来看看我们路径压缩的优化效果。1
2
3
4
5UnionFind3 : 4.289546148s
UnionFind4 : 4.266191791s
UnionFind5 : 3.837546687s
Process finished with exit code 0
我们进行路径压缩的过程中,其实我们树的高度是降低的,但是并没有去维护rank数组的值,其实这是合理的,这也是这个数组取名rank,而不是height的原因,它表示的其实是一个排名,当我们进行路径压缩的时候,这个rank就不是严格意义上的树的高度了,它仅代表了树的一个排名。同一棵树不同节点对应的rank值可能是不同的,但是整体上的排名是一定的,这个排名依然可以用作union操作判断的依据。这里不做rank的维护,也是出于对性能的考虑,不维护的情况下已经可以胜任判断排名的依据,就无需费时去管理每一个节点的rank值使同一棵树的节点rank保持一致。
以上,我们一步步优化,实现了5个版本的并查集,相信还有不同思路的优化实现,比如路径压缩有很多种方法,我们只实现了一种,还可以使用递归来实现等等。
到此为止,并查集的内容就介绍完了,记录下学习的历程,相信对自己也是很大的提高。